Бинарное дерево поиска — это структура данных, в которой выполняются три свойства:
- Элементы в левом поддереве должны быть меньше родительского узла.
- Элементы в правом поддереве должны быть больше родительского узла.
- У каждого узла не больше двух потомков.
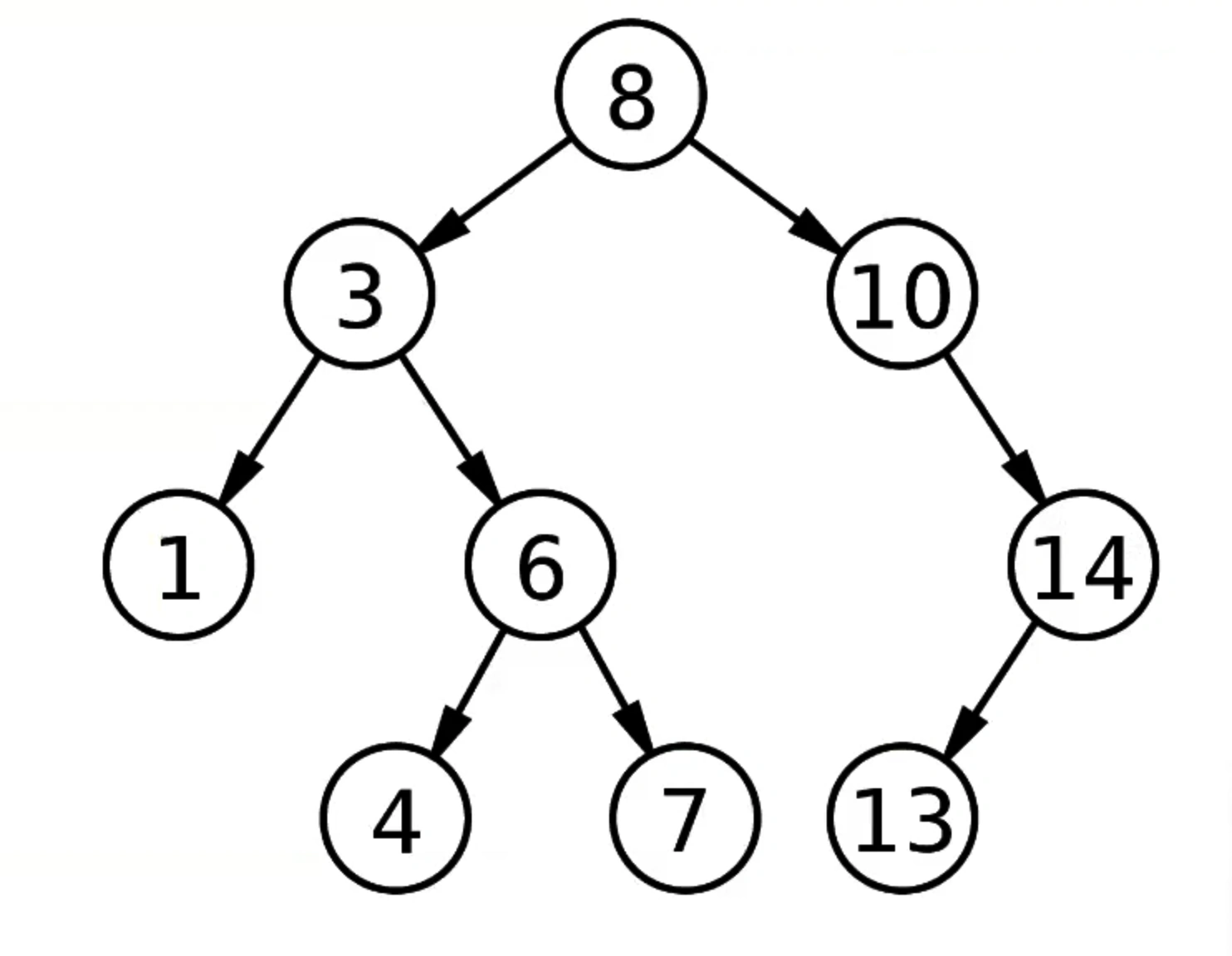
Эти свойства обеспечивают:
- Гарантированный порядок элементов.
- Детерминированный алгоритм поиска.
- В вырожденном случае придется посетить все элементы — сложность O(n).
Сбалансированное дерево
Чтобы улучшить поиск, можно использовать сбалансированное бинарное дерево.
Сложность операций
- Средний случай: поиск, вставка и удаление выполняются за O(log n), если дерево сбалансировано.
- Худший случай: если дерево становится несбалансированным, операции могут иметь сложность O(n). Это происходит, когда элементы добавляются в возрастающем или убывающем порядке, превращая дерево в цепочку.
Основные операции с бинарным деревом поиска
Вставка
При вставке нового элемента в бинарное дерево поиска он помещается в соответствующее место таким образом, чтобы сохранялся порядок элементов. Например, если вставляется значение 15, и оно меньше текущего узла, оно вставляется в левое поддерево, иначе — в правое.
Удаление
Удаление элемента из бинарного дерева поиска может потребовать нескольких шагов, чтобы сохранить его свойства:
- Удаление листа: просто удаляется узел.
- Удаление узла с одним потомком: узел заменяется своим потомком.
- Удаление узла с двумя потомками: узел заменяется минимальным значением в правом поддереве или максимальным значением в левом поддереве.
Поиск
Поиск элемента в бинарном дереве поиска выполняется путем рекурсивного или итеративного перехода по узлам, начиная с корня. Если искомое значение меньше текущего узла, поиск продолжается в левом поддереве, если больше — в правом.
Обход дерева
- In-order обход: обходит узлы в порядке возрастания значений. Используется для получения отсортированного списка элементов дерева.
- Pre-order обход: сначала посещается корень, затем левое и правое поддеревья. Полезно для копирования дерева.
- Post-order обход: сначала посещаются оба поддерева, затем корень. Используется для удаления дерева.
Мета информация
Область:: 00 Разработка
Родитель:: Tree
Источник::
Автор::
Создана:: 2024-01-29