B-tree

Сбалансированное сильно-ветвистое дерево позволяет хранить в узле множество значений, что делает его эффективным для работы с большими объемами данных.

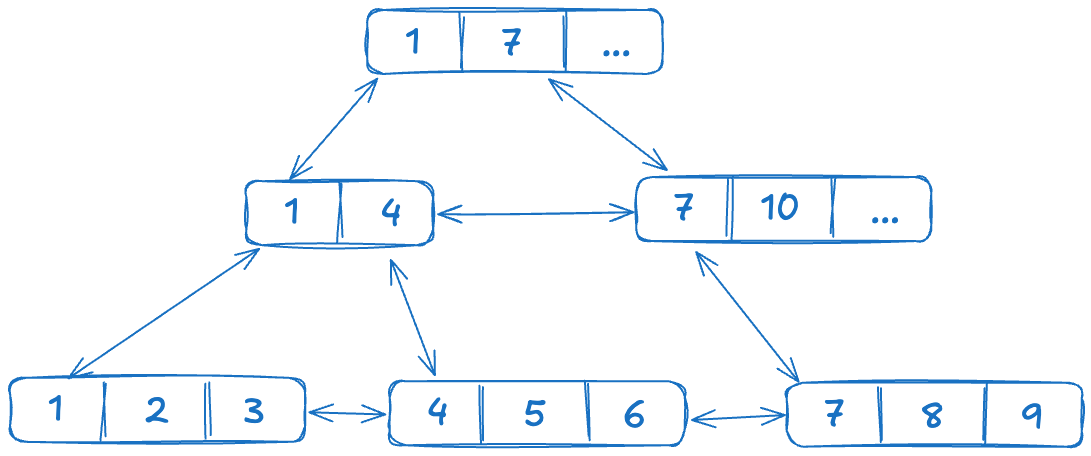
Структура B-tree индекса.excalidraw

Основные особенности B-tree

• Узел содержит множество элементов, что позволяет хранить больше данных в одном месте.
• Каждый узел представляет собой страничку на диске, что снижает издержки на чтение.
• В каждом узле есть ссылки на следующий и предыдущий узлы (характерно для B+tree). Это сильно помогает с поиском по диапазонам.
• В листьях дерева могут храниться сами данные или указатели на данные, то есть ссылаются на таблицу.
• Элементы в узле отсортированы, что делает поиск более эффективным и позволяет создавать деревья с небольшой высотой, тем самым уменьшая количество обращений к диску.
• Значения в узлах могут быть не уникальными.
• Обычно высота дерева не больше 3-4 уровней.

Параметр t

Параметр t определяет количество элементов в узле дерева.

• В каждом узле должно быть не менее t-1 и не более 2t-1 ключей. Это правило важно для поддержания сбалансированности дерева, так как позволяет равномерно распределять элементы между узлами и поддерживать эффективную высоту дерева, что, в свою очередь, обеспечивает высокую производительность операций поиска.
• Это правило не выполняется для корневого узла.

Как выбрать t: значение t влияет на высоту дерева — большее значение уменьшает высоту, что снижает количество обращений к диску. Обычно t выбирается в диапазоне от 50 до 2000 в зависимости от размера блока на диске и объема оперативной памяти. Например, при t = 1001 и 1 млрд записей требуется всего 3 операции для поиска любого ключа.

Применение B-tree

С чем может помочь:

• Поиск по равенству: a = 5
• Поиск по открытому диапазону: a > 5 или a < 3
• Поиск по закрытому диапазону: 3 < a < 8
• LIKE работает с индексами по префиксам (LIKE 'a%' — эффективно)
  С чем НЕ поможет:
• Поиск четных или нечетных чисел.
• Поиск суффиксов (LIKE '%c' — неэффективно).

Поиск в B-tree

Алгоритм поиска аналогичен бинарному дереву, но выбор осуществляется из нескольких вариантов, а не из двух. Поиск выполняется за O(t logt(n)), но количество обращений к диску — O(logt(n)).

Рассмотрим пример поиска значения 5. Начинаем с корневого узла, он всегда один. 5 больше 1, но меньше 7, поэтому идем в левую часть дерева.

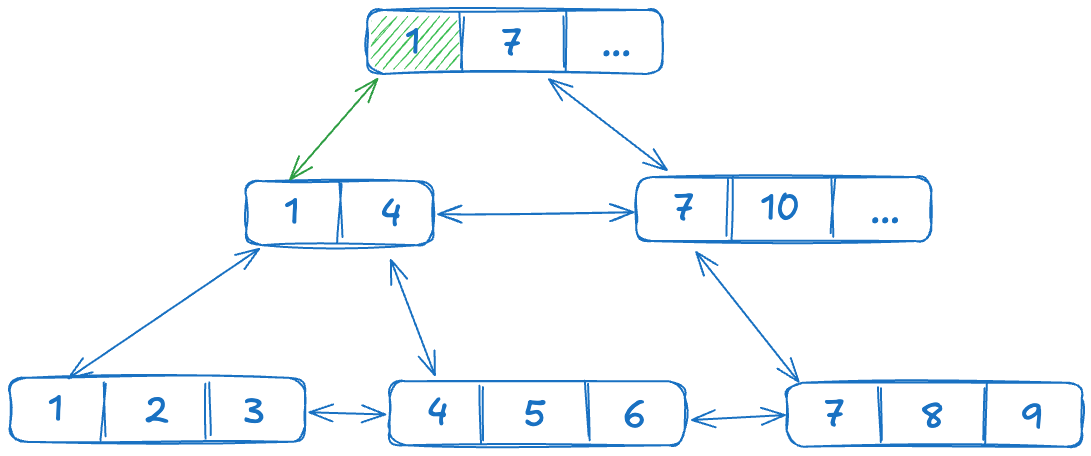
Поиск в B-tree индексе 1.excalidraw

Видим, что 5 больше чем 4, поэтому идем по ссылке на 4.

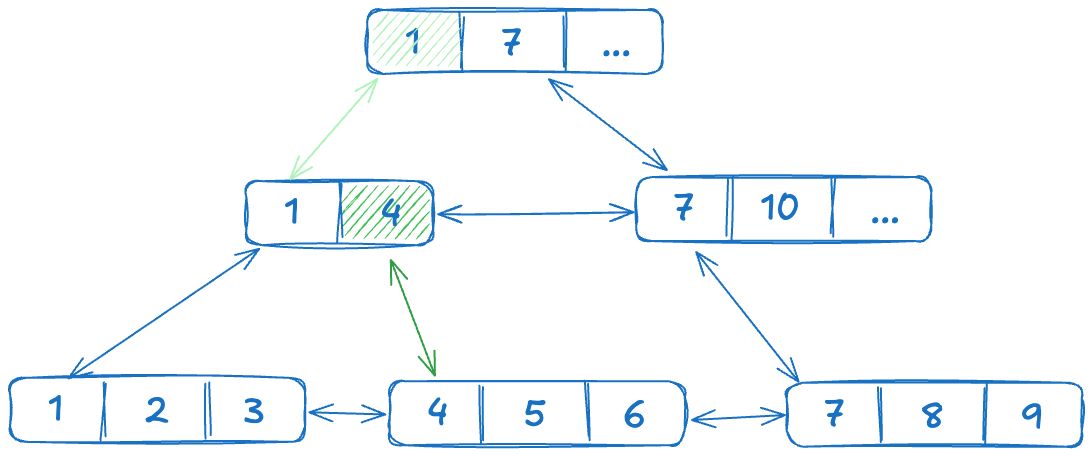
Поиск в B-tree индексе 2.excalidraw

И там уже мы находим нашу 5.

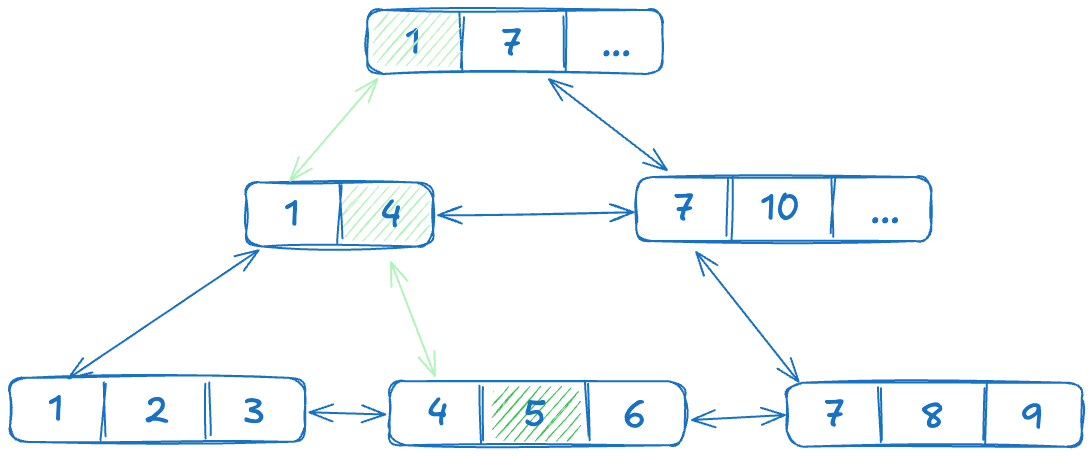
Поиск в B-tree индексе 3.excalidraw

Значения в узлах могут быть не уникальными. Например, если значение 5 встречается дважды, поиск продолжается, переходя в следующий узел. Чтобы облегчить этот процесс, блоки на одном уровне связаны, создавая связный список.

Добавление в B-tree

Представим, что нужно вставить значение 15 в уже существующее дерево.

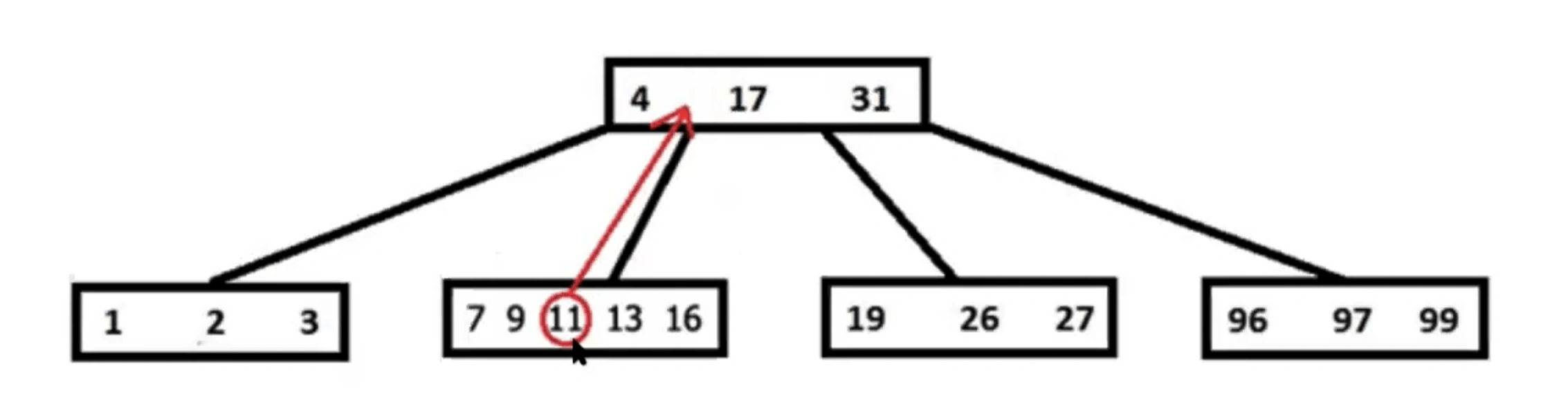
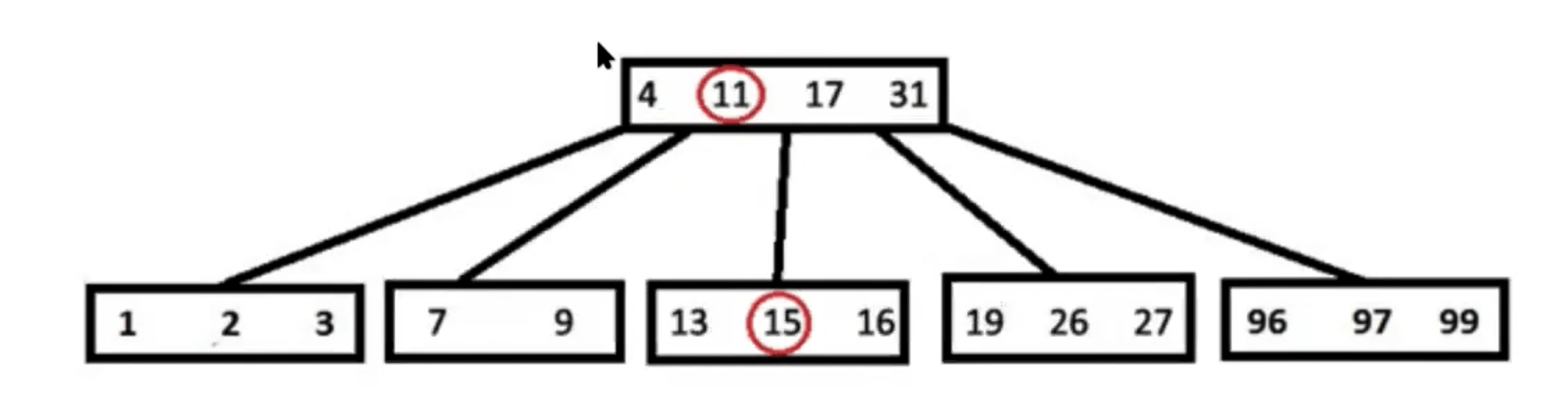
Вставка должна произойти между значениями 4 и 17. Узел 7...16 переполнен (t = 3, максимум 5 значений), поэтому узел разбивается начиная с t-1 элемента (в данном случае 11). Элемент, по которому происходит разбиение, перемещается в родительский узел. Если родительский узел переполняется, он тоже разбивается, и так далее.

После вставки мы получим следующее дерево

Удаление из B-tree

Удаление элемента из B-tree требует поддержания минимального количества ключей в узле для сохранения сбалансированности дерева и его эффективной высоты. Например, при удалении элемента, если количество ключей в узле становится меньше t-1, выполняется перераспределение элементов из соседних узлов или их слияние, чтобы поддерживать сбалансированность. Существует несколько сценариев удаления:

• Удаление из листового узла: Если элемент находится в листовом узле и после его удаления остается не менее t-1 элементов, узел остается без изменений.
• Удаление из внутреннего узла: Если удаляемый элемент находится во внутреннем узле, он заменяется на наибольший элемент в левом поддереве или наименьший элемент в правом поддереве. После этого выполняется удаление из листового узла.
• Перераспределение и слияние узлов: Если после удаления в узле остается меньше t-1 элементов, выполняется перераспределение элементов из соседнего узла или слияние с соседним узлом.

Мета информация

Область:: 00 Разработка, 00 Алгоритм
Родитель:: Tree
Источник::
Автор::
Создана:: 2024-01-29

Дополнительные материалы

Дочерние заметки